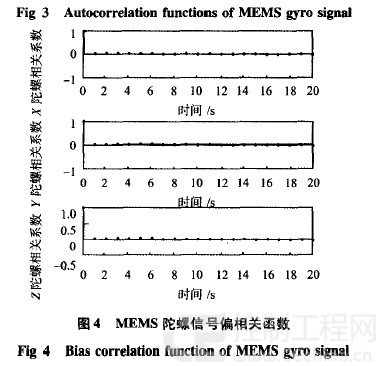
3)模型阶次的确定
        从上面的分析已经可以确定漂移模型的形式，但为了确定模型的阶数，还得借助PPE准则或者AIC准则，寻找 使PPE准则或者AIC准则取最小值的模型，确定最适合的 模型和阶次，以 陀螺为例，表2给出所有适合的模型系数 AIC的值。

        从表2中可以看出：AIC值差别不大，从工程实用的角 度，选择AR(1)模型作为陀螺随机漂移的模型。
        4)建立随机误差的系统方程
        陀螺漂移是一个随机平稳过程，根据上面的分析，对X 陀螺用AR(1)模型来描述

        (3) 其中， (k)是漂移模型的状态，W(k)是均值为零，方差 为0．6185(由实际数据计算)的白噪声，从系统的观点出 发，认为漂移是以白噪声为输入的系统的输出。
        其中，∞ 为陀螺角速率；q 为AR模型对应的随机漂 移部分。系统的观测值Y(k)可以表示为状态量加上观测 噪声lCONTROL ENGINEERING China版权所有，(k)，／．p(k)是均值为0，方差为2．952 7的白噪声，卡 尔曼滤波的观测方程为

        其中，∞ 为陀螺角速率；q 为AR模型对应的随机漂 移部分。系统的观测值Y(k)可以表示为状态量加上观测 噪声lCONTROL ENGINEERING China版权所有，(k)，／．p(k)是均值为0，方差为2．952 7的白噪声，卡 尔曼滤波的观测方程为

        为了更进一步说明方法的正确性，将系统放置在三轴 转台上，以l0。／s的角速率转动，采集数据30 S，采样频率为 2OHzCONTROL ENGINEERING China版权所有，对实验数据进行分析，滤波结果如图7所示，可以看 出：在动态下具有和静态下一致的效果。

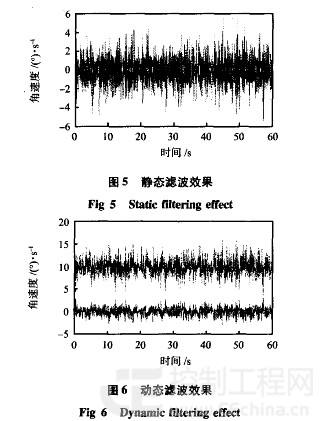
        经计算，滤波前的测量数据方差为0．422 1，滤波后估 计值的方差为0．1324，为滤波前的31．35％ ，滤波效果明 显，它可以满足实时性的要求。
        5 结论
        通过对自研的MEMS捷联惯导系统的研究，分别对 MEMS陀螺的确定性误差和随机误差进行了辨识和补偿， 通过建立随机误差的AR模型，采用卡尔曼滤波进行了补 偿，并在动态下进行了验证，无论静态还是动态下，补偿后 的信号方差优于补偿前的3O％ ，说明了建模方法正确，滤 波效果明显，具有一定的工程应用价值。 ’ ·
        参考文献：
        [1] 李荣冰，刘建业．基于MEMS技术的微型惯性导航系统的发 展现状[J]．中国惯性技术学报，2004(6)：88-94．
        [2] 吉训生，王寿荣．MEMS陀螺仪随机漂移误差研究[J]．宇航 学报，2006，27(4)：640—642．
        [3] Shkel A M．Type I and Type II micro machined vibratory gym— scope[c]∥Proceeding of Position。Location and Navigation Sys— tern，2006．
        [4] 杨叔子，吴雅．时间序列分析的工程应用[M]．武汉：华中 理工大学出版社，1996．
        [5] 张树侠．激光陀螺漂移的数据建模和滤波[J]．中国惯性技术 学报，1999，17(4)：70-72．
        [6] 张树侠，闫威．激光陀螺漂移的数据建模和滤波[J]．中国 惯性技术学报，1999，7(4)：21-25．
        [7] 吉训生，王寿荣，许宜申．自适应Ka|man滤波在MEMS陀螺 仪信号处理中的应用[J]．传感器与微系统，2006，25(9)： 79—82．